다익스트라 알고리즘 (Greedy)

다익스트라 알고리즘은 최단 경로에 자주 사용되고 여러 코딩 테스트 문제에도 자주 등장한다.
매번 공부하지만 계속 까먹어서 이참에 상세히 정리해보려 한다.

다익스트라 알고리즘의 개념

다익스트라 알고리즘

SSSP (Single Source Shortest Path) 를 구하기 위해서 사용되는 알고리즘이다.
다익스트라 알고리즘은 사이클이 없는 방향성 그래프에 한해서만 사용할 수 있다.

다익스트라 알고리즘의 동작 원리

각 정점에는 시작점으로부터 자신에게 이르는 경로의 길이를 저장할 곳을 준비하고 각 정점에 대한 경로의 길이를 무한대로 초기화 한다.
시작 정점의 경로 길이를 0으로 초기화하고 (시작 정점에서 시작 정점까지의 길이는 0이다) 최단 경로에 추가한다.
최단 경로에 새로 추가된 정점의 인접 정점에 대해 경로 길이를 갱신하고 (경로가 아무리 길어도 무한대보다는 짧다) 이들을 최단 경로에 추가한다. 만약 추가하려는 인접 정점이 이미 최단 경로 안에 있다면, 갱신되기 이전의 경로 길이가 새로운 경로 길이보다 더 큰 경우에 한해 다른 선행 정점을 지나던 기존 경로가 현재 정점을 경유하도록 수정한다.
그래프 내 모든 정점이 최단 경로에 소속될 때 까지 단계 3의 과정을 반복한다.

다익스트라 알고리즘 직관

배열로 이해하기

정점 개수 N인 그래프가 있을 때, graph[i][j]는 정점 i에서 j로 가는 간선의 가중치(비용)를 저장한다.
연결이 없으면 ∞(무한대), 자기 자신은 0으로 채운다.

	1	2	3	4	5
1	0	6	3	10	∞
2	∞	0	2	∞	∞
3	∞	∞	0	1	∞
4	∞	∞	∞	0	7
5	5	4	∞	∞	0

다익스트라 알고리즘 단계별 동작

(1) 초기화

distance[시작점] = 0, 나머지는 ∞
visited[시작점] = True

정점	1	2	3	4	5
거리	0	∞	∞	∞	∞
방문	O	X	X	X	X

(2) 인접 행렬을 이용해 인접 노드 거리 갱신

시작점(1번)에서 직접 연결된 정점의 최단 거리를 갱신한다.

정점	1	2	3	4	5
거리	0	6	3	10	∞
방문	O	X	X	X	X

(3) 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 선택

3번(거리 3)이 가장 짧으므로 방문 처리

정점	1	2	3	4	5
거리	0	6	3	10	∞
방문	O	X	O	X	X

(4) 선택한 노드(3번)의 인접 노드 거리 갱신

3번에서 4번으로 가는 간선(1)이 있으므로,

기존 4번 거리(10)와 (3+1=4) 중 작은 값으로 갱신

정점	1	2	3	4	5
거리	0	6	3	4	∞
방문	O	X	O	X	X

(5) 위 과정을 반복

방문하지 않은 노드 중 거리 최소(4번, 4) 방문 → 인접 5번(4+7=11)로 갱신
방문하지 않은 노드 중 거리 최소(2번, 6) 방문 → 인접 3번(6+2=8, 이미 3번의 거리가 3이므로 갱신 X)
방문하지 않은 노드 중 거리 최소(5번, 11) 방문 → 종료

최종 거리 배열:

정점	1	2	3	4	5
거리	0	6	3	4	11
방문	O	O	O	O	O

그림으로 알아보기

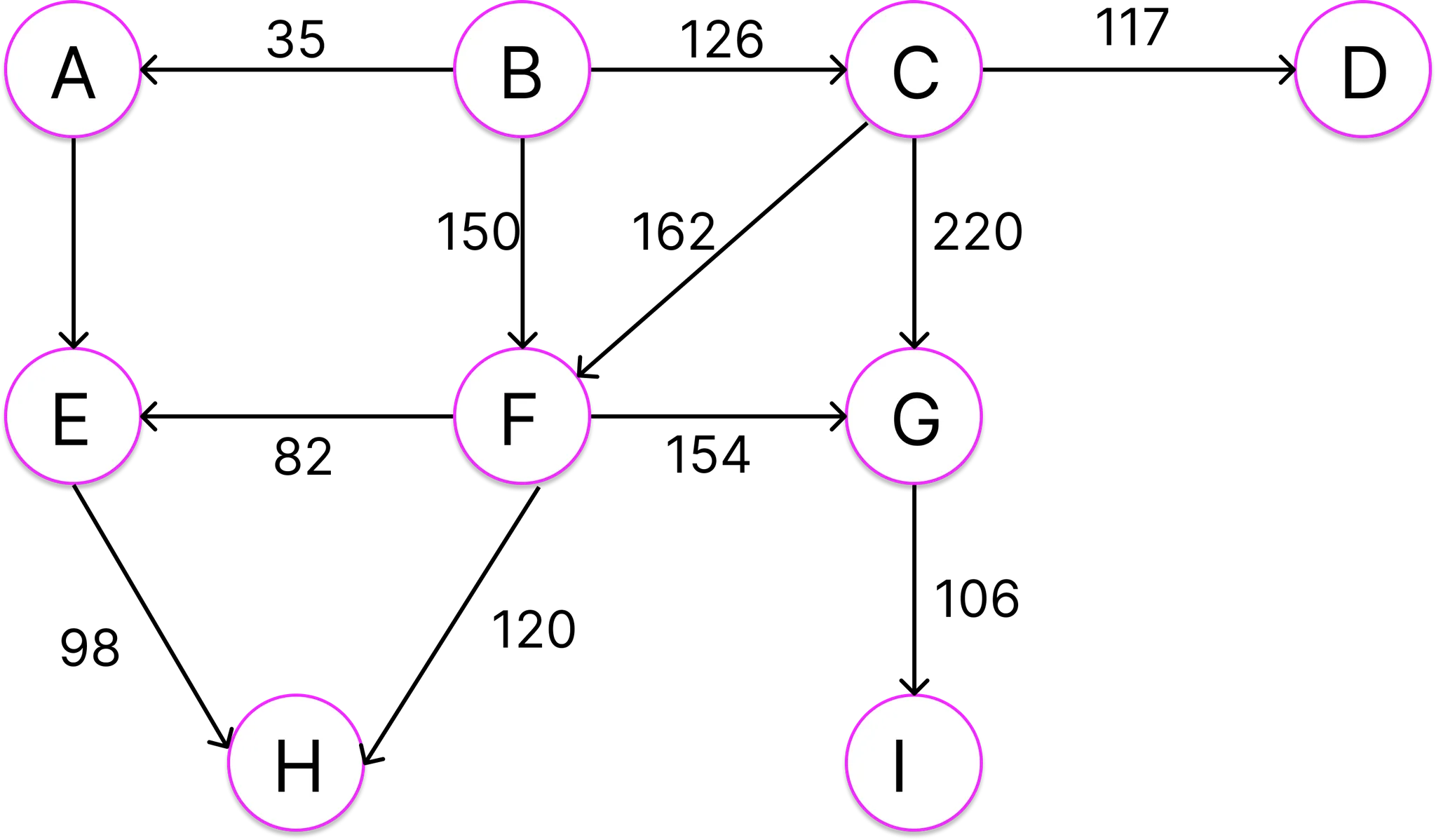
경로는 시작점과 도착점을 갖는다. 다익스트라 알고리즘 역시 시작점과 도착점을 필요로 한다. 이 예제에서는 B를 시작점으로 설정하고 ‘나머지 모든 정점’을 도착점으로 지정한다.

우선 각 정점별로 경로 길이를 좌측 상단의 상자 안에 표시하고 초기값을 무한대로 설정한다. 그리고 시작 정점 B의 경로 길이는 0으로 바꾼다.

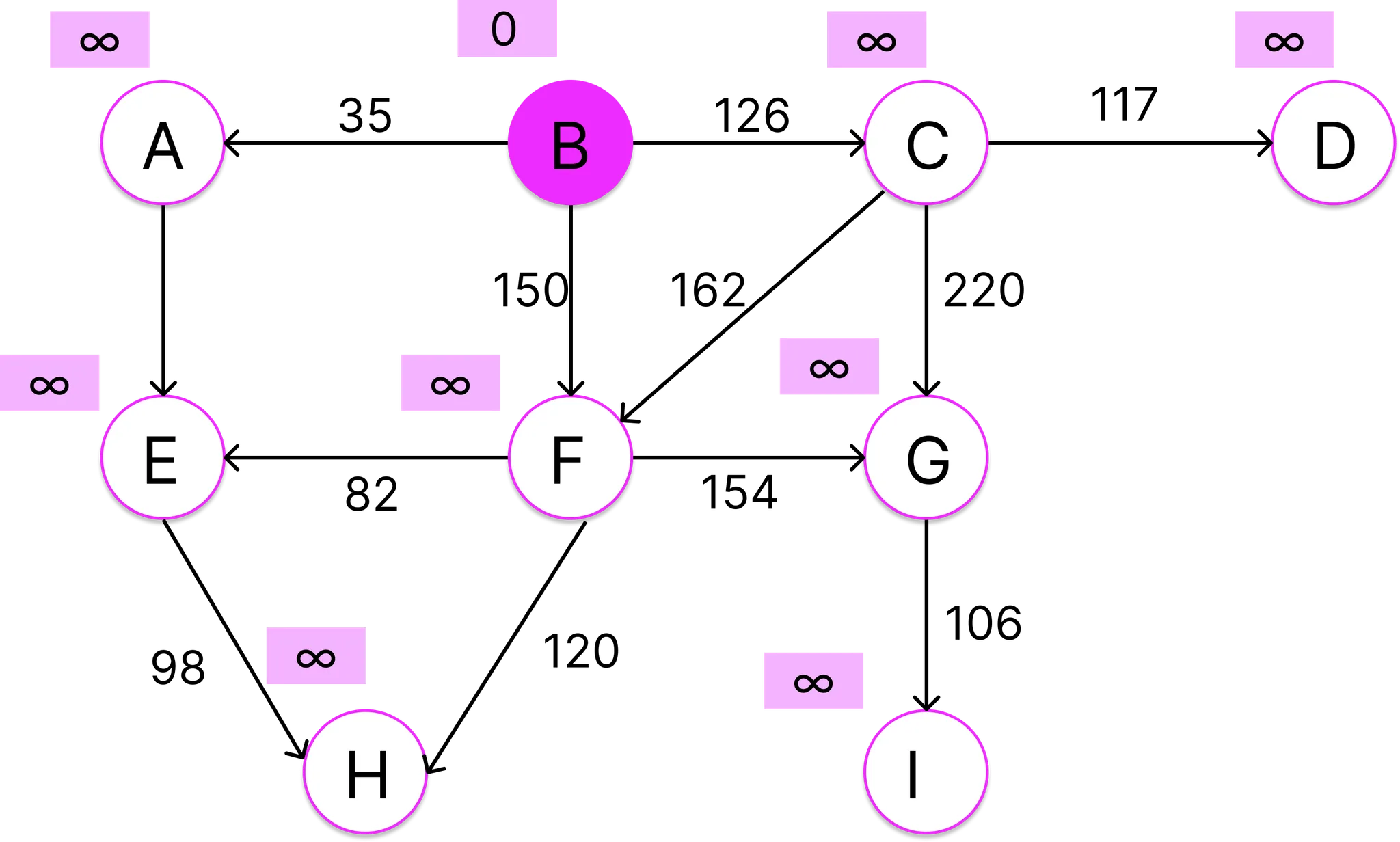
시작 정점인 B에 인접합 정점들을 찾고 간선의 가중치를 표시한다. 정점 A,C,F가 B에 인정해 있고 각각의 경로의 길이를 수정해준다.

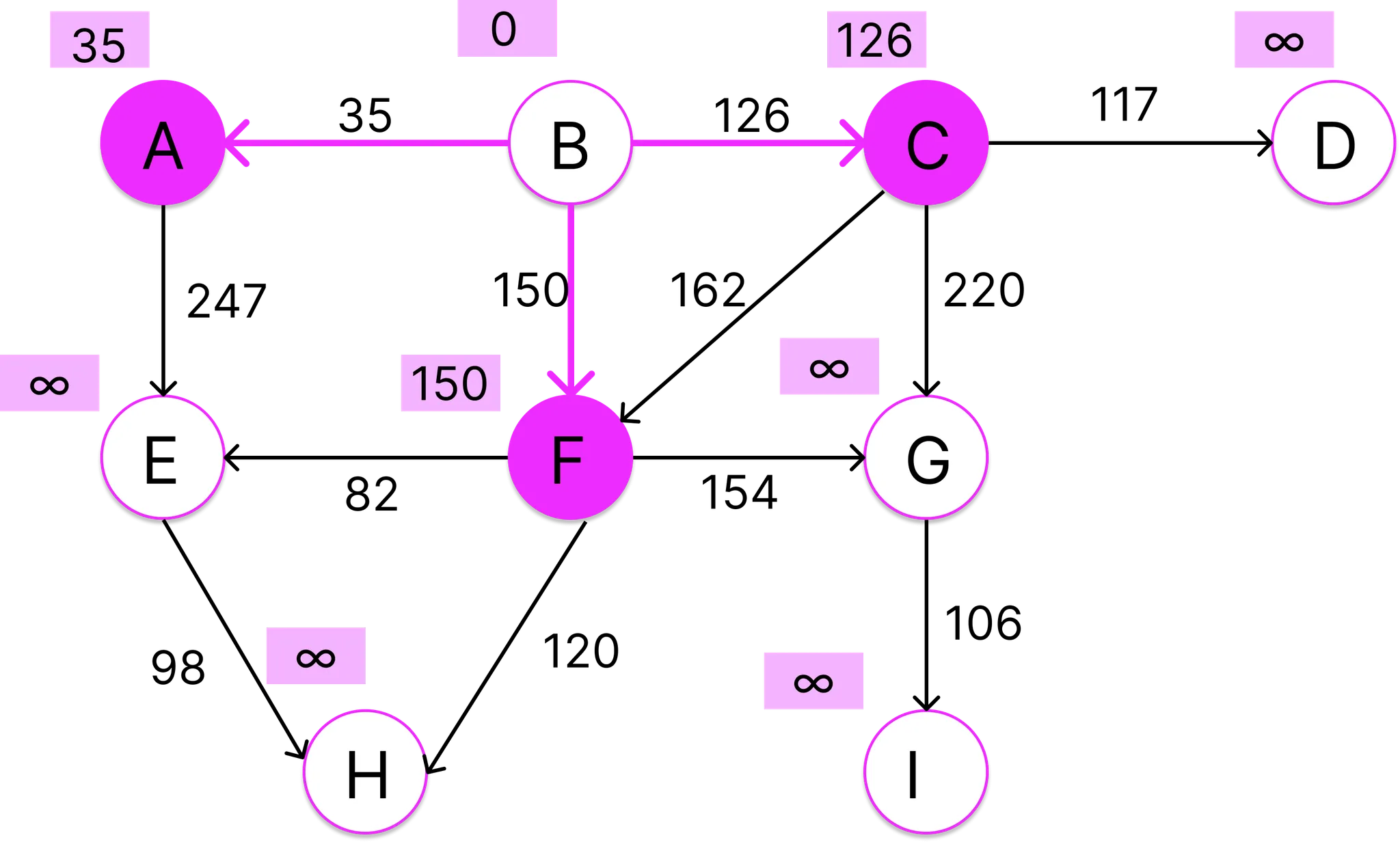
현재까지 확보된 정보에 의하면 정점 B에서 E로 갈 수 있는 길을 B-A-E가 유일하다 (B-F-E 경로는 발견하지 못한 상태이다). B-A까지는 35가 들고, A-E로 이동하는데에는 247이 든다. 따라서 A의 경로 길이 35와 간선 A-E의 비용 282를 경로 길이로 입력한다. 이 값은 무한대보다 작으므로 입력 가능하다.

이제 C의 인접 정점들을 조사할 차례이다. C의 인접 정점은 D,F,G가 있는데 현재 D의 경우 길이는 무한대이므로 B-C-D의 경로의 비용을 그대로 입력하고 G 역시 길이가 무한대 이므로 B-C-G 경로의 비용을 입력하며 된다. 주의 깊게 봐야 할 부분은 정점 F인데, 현재 F가 가진 경로의 길이는 150이므로 B-C-F 경로의 비용인 288보다 작다. 따라서 새로 발견한 경로 B-C-F는 B-F보다 비용기 크기 때문에 채택 할 수 없다.

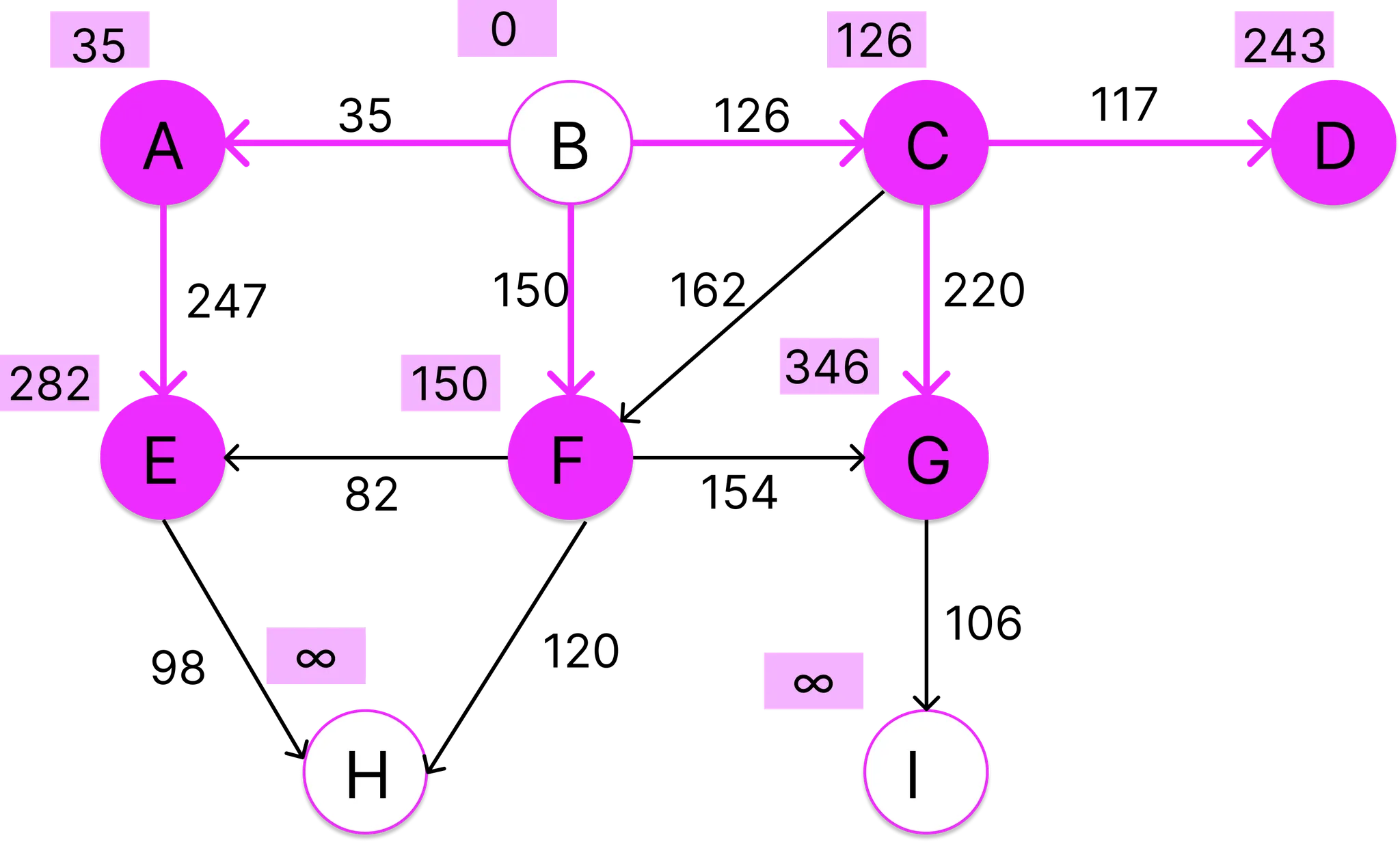
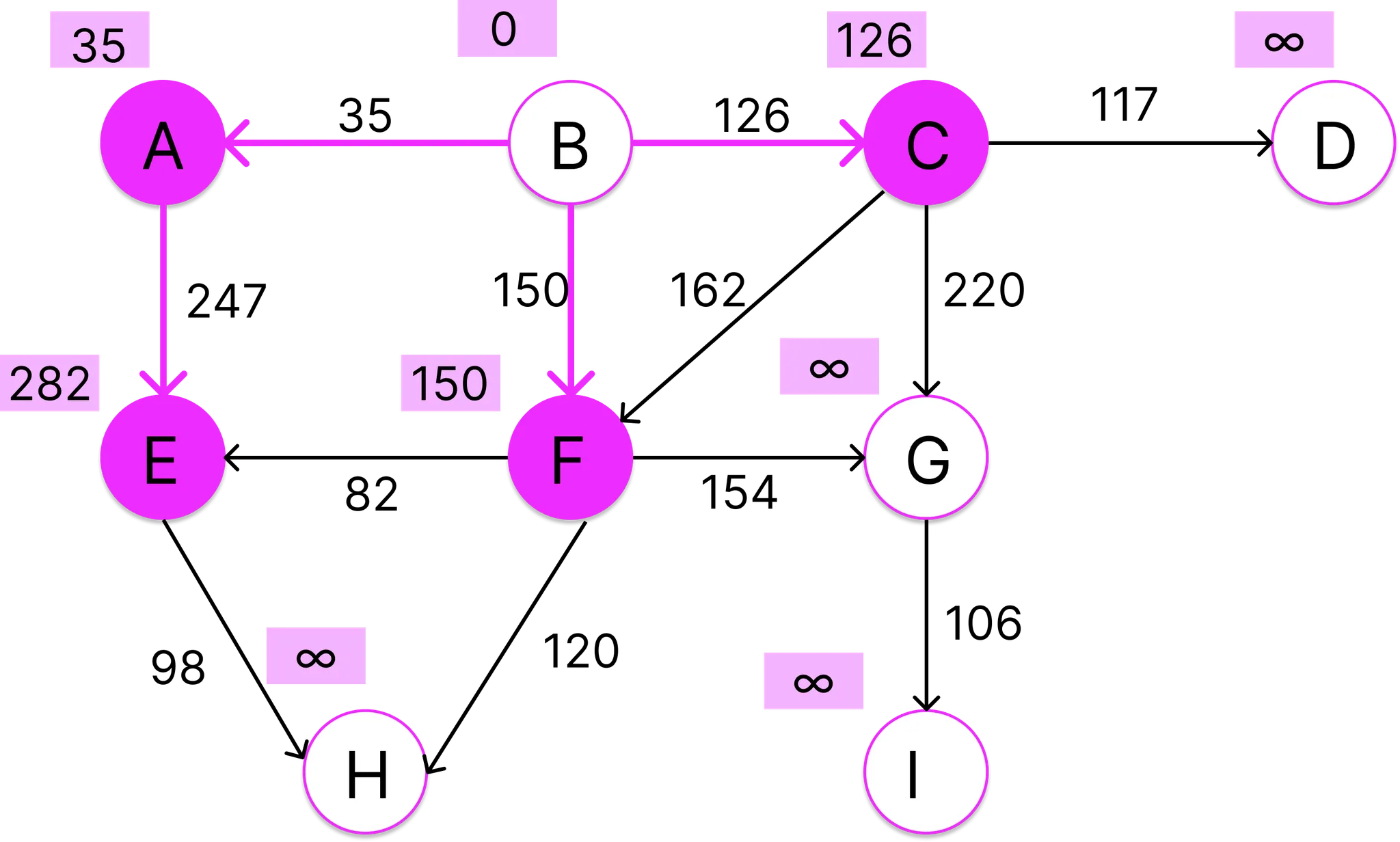
이번에는 정점 F에 인접한 정점들을 살펴보자. F는 E,G,H와 이웃하고 있다. 먼저 E를 보면, 기존 경로의 길이가 282인데 새로운 경로 B-F-E의 비용이 232로 더 작다. 따라서 B-A-E는 폐기하고 새로운 경로 B-F-E를 채택한다. G도 마찬가지로 기존의 경로 B-C-G (346) 보다 새 경로 B-F-G (304)가 훨씬 저렴하므로 예전 것을 폐기하고 새로운 경로를 채택한다. H의 경로의 길이는 현재 무한대 이므로 B-F-H의 비용 270을 경로 길이로 입력한다.

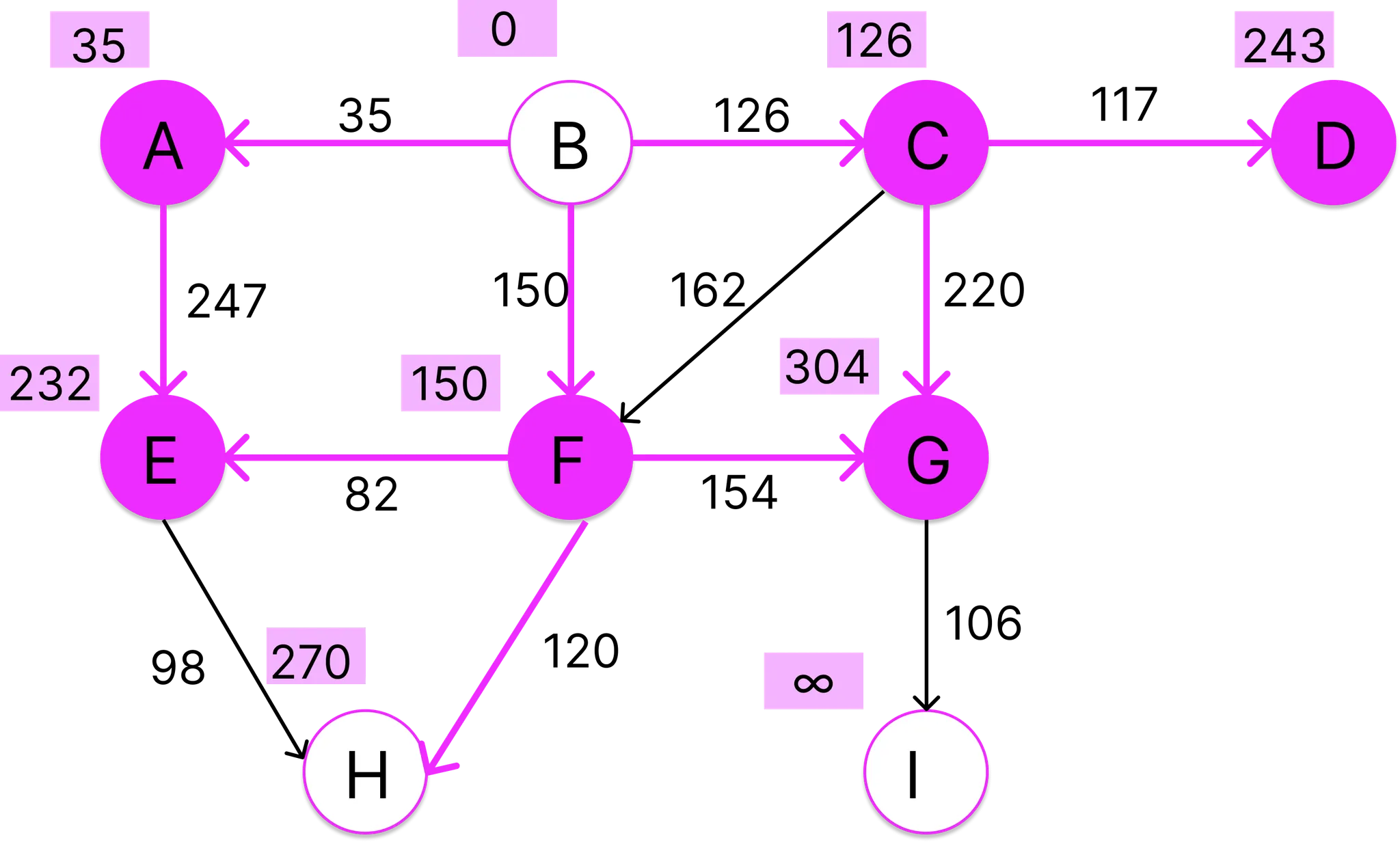
E의 인접 정점 H가 있기는 하지만 경로 B-F-E-H의 비용이 330이고, 현재 경로 길이 270보다 크기 때문에 넘어간다. 이제 정점 G만 유일하게 방문하지 않은 정점 I를 갖고 있는데, I의 현재 경로 길이는 무한대 이므로 경로 B-F-G-I의 비용 410을 입력한다.

이제 더 탐사할 노드가 없으므로 최단 경로 탐색을 종료한다.

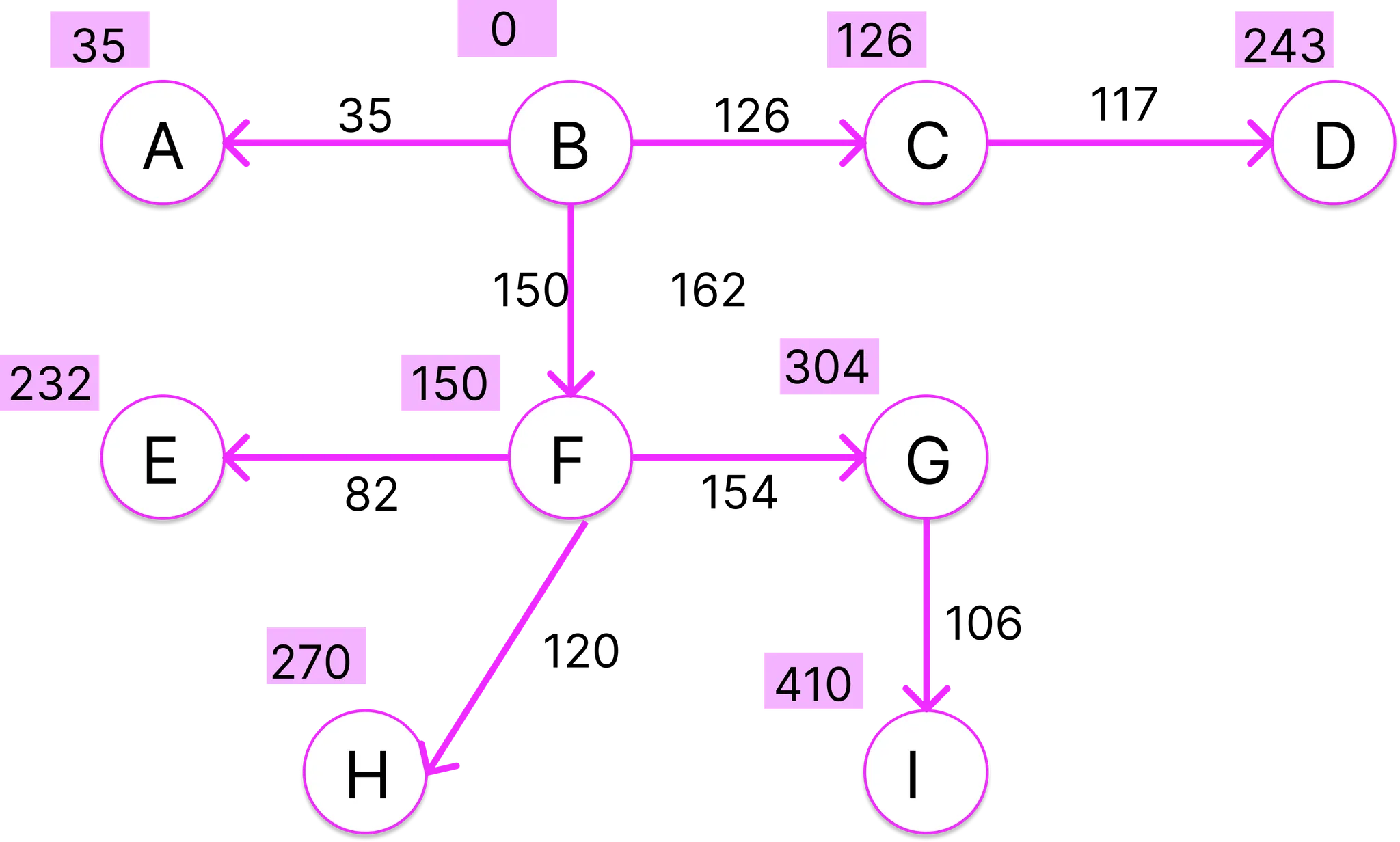
분석

시간 복잡도 분석

단순 배열/선형 탐색 사용 시

방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 매번 선형 탐색으로 찾는다.
각 단계마다 O(V), 전체 V번 반복 → O(V²)
시간 복잡도: O(V$^2$)
노드 수가 적을 때(수천 개 이하)만 실용적이다

우선순위 큐(힙) 사용 시

최단 거리가 가장 짧은 노드 선택을 힙(우선순위 큐)으로 빠르게 처리한다.
각 간선에 대해 힙에 삽입/삭제 연산이 O(log V)
모든 간선(E)에 대해 연산이 일어나므로
시간 복잡도: O(Elog⁡V)
실제로는 O((V+E)logV)로 표기하기도 하지만, 일반적으로 O(E log V)로 쓴다

그리디 관점에서의 다익스트라

다익스트라 알고리즘은 그래프 내의 한 정점에서 다른 정점으로 향하는 가장 짧은 경로를 구하는 알고리즘이다. 다익스트라 알고리즘은 아래와 같이 동작한다.
1. 강 정점에는 시작점으로부터 자신에게 이르는 경로의 길이를 저장할 곳을 준비하고 각 정점에 대한 경로의 길이를 무한대로 초기화 한다.
2. 시작 정점의 경로 길이를 0으로 초기화하고 (시작 정점에서 시작 정점까지의 길이는 0이다) 최단 경로에 추가한다.
3. 최단 경로에 새로 추가된 정점의 인접 정점에 대해 경로 길이를 갱신하고 (경로가 아무리 길어도 무한대보다는 짧다) 이들을 최단 경로에 추가한다. 만약 추가하려는 인접 정점이 이미 최단 경로 안에 있다면, 갱신되기 이전의 경로 길이가 새로운 경로 길이보다 더 큰 경우에 한해 다른 선행 정점을 지나던 기존 경로가 현재 정점을 경유하도록 수정한다.
4. 그래프 내 모든 정점이 최단 경로에 소속될 때 까지 단계 3의 과정을 반복한다.
위 알고리즘에서 단계 1, 2는 알고리즘의 초기화 작업에 해당되며 단계 3과 4가 본격적으로 최단 경로를 만드는 과정이다. 단계 3은 해 선택과 실행 가능성 검사, 단계 4는 해 검사를 맡는다.
다익스트라 알고리즘을 살펴보면 이 알고리즘이 한 정점의 인접 정점들에 대해 정보만 이용하여 최단 경로를 구축해나간다는 사실을 확인 할 수 있다. 이것은 다시 말하면 다익스트라 알고리즘은 근시안적인 접근법을 이용하여 문제를 해결한다는 뜻이다.

증명

증명은 아래 블로그를 참고해보자! 굉장히 잘 정리가 되어 있다. 다익스트라의 알고리즘 (Dijkstra's Algorithm)

코드로 알아보기

Relax 함수

Relax는 어떤 간선 (u,v)에 대해, 현재까지 알려진 출발점에서 v까지의 최단 거리(d[v])가, u를 거쳐서 v로 가는 거리(d[u]+w(u,v))보다 크다면, 더 짧은 경로를 발견했으므로 d[v] 값을 갱신(업데이트)하는 연산이다

Relax 함수의 동작 원리

현재까지의 d[v] (출발점에서 v까지의 최단 거리 추정치)와
u를 거쳐 v로 가는 거리 d[u]+w(u,v)(여기서 w(u,v)는 간선의 가중치)를 비교한다.
만약 d[v]>d[u]+w(u,v)라면,
- d[v]를 d[u]+w(u,v)로 갱신한다.
- 필요하다면 v의 이전 정점 정보(경로 추적용)도 함께 갱신한다

function relax(u, v, w):
    if d[v] > d[u] + w(u, v):
        d[v] := d[u] + w(u, v)

각 단계별 설명

초기화
- **S**는 아직 최단 경로가 확정되지 않은 정점 집합(비어 있음)
- **Q**는 모든 정점을 담은 우선순위 큐(최단 거리 기준)
- **Initialize(G, s)**는 시작점 s의 거리 d[s]=0, 나머지 d[ ]=∞로 설정
메인 루프
- **Q**가 빌 때까지 반복
- EXTRACT-MIN(Q): Q에서 d[u]가 가장 작은 정점 u를 꺼냄(최단 경로가 확정된 정점)
- **S**에 u를 추가
이웃 정점 Relax
- u의 모든 인접 정점 v에 대해
- RELAX(u, v, w): u를 거쳐 v로 가는 경로가 더 짧으면 d[v]를 갱신(릴랙스 연산)

Dijkstra(G, W, s)   // G: 그래프, W: 가중치, s: 시작 정점
    // 1. 초기화
    S ← ∅                   // 최단 경로 확정 집합
    Q ← V[G]                // 모든 정점을 Q(우선순위 큐)에 삽입
    Initialize(G, s)        // 시작점 s에 대해 d[s]=0, 나머지는 d[ ]=∞
 
    // 2. 본격적인 반복
    while Q ≠ ∅ do
        u ← EXTRACT-MIN(Q)  // Q에서 d[u]가 가장 작은 정점 u를 꺼냄
        S ← S ∪ {u}         // u를 최단 경로 확정 집합에 추가
 
        for each v ∈ Adj[u] do
            RELAX(u, v, w)  // u를 거쳐 v로 가는 더 짧은 경로가 있으면 갱신

구현 (C++) - 인접 행렬

포인트 1. 큐에서 꺼낸 거리가 기존 거리보다 길 경우, 스킵한다
포인트 2. 우선순위큐에 pair를 넣게 되면, 첫번째 요소를 기준으로 비교한다
포인트 3. 큐에 넣을 때는 방문하지 않은 노드만을 넣는게 아니라, 거리가 갱신 될 경우 다 넣는다.

#include <iostream>
#include <string>
#include <vector>
#include <climits>
#include <queue>
#include <numeric>
#include <algorithm>
#include <set>
 
using namespace std;
 
int main() {
 
	// 노드 수, 간선 수
	int N, M;
 
	cin >> N >> M;
 
	vector<vector<int>> graph_list(N + 1, vector<int>(N + 1, INT_MAX));
 
	vector<int> distance(N + 1, INT_MAX);
 
	for (int i = 0; i < M; i++) {
		int start, dest, weight;
		cin >> start >> dest >> weight;
		graph_list[start][dest] = weight;
		graph_list[dest][start] = weight;
	}
 
	// 우선 순위 큐 저장 - 1번이 시작 노드라고 가정
	priority_queue<pair<int, int>> q;
	distance[1] = 0;
 
	// 거리, 노드 순
	q.push({ 0, 1 });
 
	while (!q.empty()) {
		// 우선 순위 큐에 pair를 넣을 경우, 첫번째 요소를 기준으로 비교연산
		int weight = q.top().first;
		int current_node = q.top().second;
		q.pop();
 
		// 예전의 정보는 버린다.
		if (distance[current_node] < weight) continue;
 
		// 최종 배열에 저장
		distance[current_node] = weight;
 
		// 인접한 노드에 대해서 relax 수행
		for (int i = 1; i <= N; i++) {
 
			int new_distance = distance[current_node] + graph_list[current_node][i];
 
			if (graph_list[current_node][i] != INT_MAX && distance[i] > new_distance) {
				q.push({ i, new_distance });
				distance[i] = new_distance;
			}
		}
	}
	for (int i = 1; i <= N; i++) {
		cout << distance[i] << '\n';
	}
}

인접 리스트

#include <iostream>
#include <vector>
#include <queue>
#include <limits>
 
// pair를 편하게 사용하기 위한 별칭 설정
using namespace std;
typedef pair<int, int> pii;
 
// C++에서 사용할 수 있는 가장 큰 정수 값으로 무한대를 표현
const int INF = numeric_limits<int>::max();
 
int main() {
    // 입출력 속도 향상
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
 
    int V, E;
    cin >> V >> E;
 
    // --- 1. 그래프 표현: 인접 리스트 방식 ---
    // 각 노드에 연결된 {도착 노드, 가중치} 쌍을 저장하는 벡터
    vector<vector<pii>> graph(V+1);
 
    for (int i = 0; i < E; ++i) {
        int u, v, w;
        cin >> u >> v >> w;
        graph[u].push_back({ v, w });
        graph[v].push_back({ u , w });
    }
 
    // 최단 거리를 저장할 배열, 모두 무한대로 초기화
    vector<int> distance(V + 1, INF);
 
    // --- 2. 최소 힙(Min Heap) 우선순위 큐 선언 ---
    // C++의 기본 priority_queue는 Max Heap이므로, 템플릿 인자를 추가하여 Min Heap으로 만듦
    // 저장되는 pair는 {거리, 노드} 순서
    priority_queue<pii, vector<pii>, greater<pii>> pq;
 
    // 시작 노드 정보 초기화
    distance[1] = 0;
    pq.push({ 0, 1 }); // {시작점까지의 거리(0), 시작 노드}
 
    while (!pq.empty()) {
        // 큐에서 가장 거리가 짧은 노드 정보를 꺼냄
        int dist = pq.top().first;
        int curr = pq.top().second;
        pq.pop();
 
        // --- 3. 낡은 정보(더 긴 경로)는 무시 ---
        // 큐에서 꺼낸 거리(dist)가 이미 기록된 최단 거리(distance[curr])보다 길다면,
        // 이 경로는 더 짧은 경로에 의해 갱신된 '낡은 정보'이므로 처리하지 않고 건너뛴다.
        if (dist > distance[curr]) {
            continue;
        }
 
        // --- 4. 실제로 연결된 간선만 효율적으로 순회 ---
        // 인접 리스트를 사용하여 현재 노드(curr)와 직접 연결된 노드들만 확인
        for (auto& edge : graph[curr]) {
            int next = edge.first;
            int weight_to_next = edge.second;
 
            // 현재 노드를 거쳐 다음 노드로 가는 것이 더 짧을 경우
            if (distance[next] > dist + weight_to_next) {
                // 거리 갱신 및 큐에 새로운 경로 추가
                distance[next] = dist + weight_to_next;
                pq.push({ distance[next], next });
            }
        }
    }
 
    // 결과 출력
    for (int i = 1; i <= V; ++i) {
        if (distance[i] == INF) {
            cout << "INF\n";
        }
        else {
            cout << distance[i] << "\n";
        }
    }
 
    return 0;
}

다익스트라 정리

다익스트라 알고리즘 (Greedy)

다익스트라 알고리즘의 개념